Quotient Properties
Learning Outcomes
- Section 9.3 Quotient of Powers Property 363 Work with a partner. How many of the smaller cubes will fi t inside the larger cube? Record your results in the table. Describe the pattern in the table. S = 4 s = 42 s 3 s = 32 c. S = 6 s = 62 s = 10 s = 102 Volume of Smaller Cube Volume of Larger Cube Larger Volume Smaller Volume.
- The Quotient Property shows that multiplying by a fraction whose numerator is 1 is the same as dividing by the denominator of that fraction, and that dividing by a number is the same as putting the divisor in.
- A special case of the Quotient Property is when the exponents of the numerator and denominator are equal, such as an expression like am am a m a m. From earlier work with fractions, we know that 2 2.
Free Algebraic Properties Calculator - Simplify radicals, exponents, logarithms, absolute values and complex numbers step-by-step This website uses cookies to ensure you get the best experience. By using this website, you agree to our Cookie Policy. Quotient of Powers Property Power of a Quotient Property Properties of Exponents. Let a and b be real numbers and let m and n be integers. Product of Powers Property Power of a Power Property Power of a Product Property Negative Exponent Property Zero Exponent Property Quotient of Powers Property Power of a Quotient Property.
- Simplify a polynomial expression using the quotient property of exponents
- Simplify expressions with exponents equal to zero
- Simplify quotients raised to a power
Simplify Expressions Using the Quotient Property of Exponents
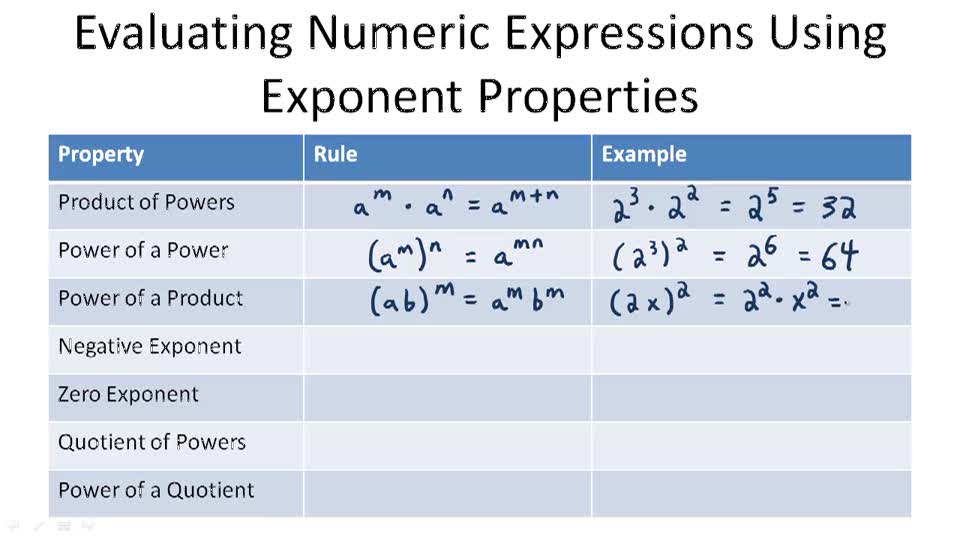
Earlier in this chapter, we developed the properties of exponents for multiplication. We summarize these properties here.
Summary of Exponent Properties for Multiplication
If [latex]atext{ and }b[/latex] are real numbers and [latex]mtext{ and }n[/latex] are whole numbers, then
[latex]begin{array}{cccc}text{Product Property}hfill & & & hfill {a}^{m}cdot {a}^{n}={a}^{m+n}hfill text{Power Property}hfill & & & hfill {left({a}^{m}right)}^{n}={a}^{mcdot n}hfill text{Product to a Power}hfill & & & hfill {left(abright)}^{m}={a}^{m}{b}^{m}hfill end{array}[/latex]
Now we will look at the exponent properties for division. A quick memory refresher may help before we get started. In Fractions you learned that fractions may be simplified by dividing out common factors from the numerator and denominator using the Equivalent Fractions Property. This property will also help us work with algebraic fractions—which are also quotients.
Equivalent Fractions Property
If [latex]a,b,c[/latex] are whole numbers where [latex]bne 0,cne 0[/latex], then
[latex]{Largefrac{a}{b}}={Largefrac{acdot c}{bcdot c}}text{ and }{Largefrac{acdot c}{bcdot c}}={Largefrac{a}{b}}[/latex]
As before, we’ll try to discover a property by looking at some examples.
[latex]begin{array}{cccccccccc}text{Consider}hfill & & & hfill {Largefrac{{x}^{5}}{{x}^{2}}}hfill & & & text{and}hfill & & & hfill {Largefrac{{x}^{2}}{{x}^{3}}}hfill text{What do they mean?}hfill & & & hfill {Largefrac{xcdot xcdot xcdot xcdot x}{xcdot x}}hfill & & & & & & hfill {Largefrac{xcdot x}{xcdot xcdot x}}hfill text{Use the Equivalent Fractions Property.}hfill & & & hfill frac{overline{)x}cdot overline{)x}cdot xcdot xcdot x}{overline{)x}cdot overline{)x}cdot 1}hfill & & & & & & hfill frac{overline{)x}cdot overline{)x}cdot 1}{overline{)x}cdot overline{)x}cdot x}hfill text{Simplify.}hfill & & & hfill {x}^{3}hfill & & & & & & hfill {Largefrac{1}{x}}hfill end{array}[/latex]
Notice that in each case the bases were the same and we subtracted the exponents.
- When the larger exponent was in the numerator, we were left with factors in the numerator and [latex]1[/latex] in the denominator, which we simplified.
- When the larger exponent was in the denominator, we were left with factors in the denominator, and [latex]1[/latex] in the numerator, which could not be simplified.
We write:
[latex]begin{array}{ccccc}frac{{x}^{5}}{{x}^{2}}hfill & & & & hfill frac{{x}^{2}}{{x}^{3}}hfill {x}^{5 - 2}hfill & & & & hfill frac{1}{{x}^{3 - 2}}hfill {x}^{3}hfill & & & & hfill frac{1}{x}hfill end{array}[/latex]
Properties Of Exponents Simplify
Quotient Property of Exponents
If [latex]a[/latex] is a real number, [latex]ane 0[/latex], and [latex]m,n[/latex] are whole numbers, then
[latex]{Largefrac{{a}^{m}}{{a}^{n}}}={a}^{m-n},m>ntext{ and }{Largefrac{{a}^{m}}{{a}^{n}}}={Largefrac{1}{{a}^{n-m}}},n>m[/latex]
A couple of examples with numbers may help to verify this property.
[latex]begin{array}{cccc}frac{{3}^{4}}{{3}^{2}}stackrel{?}{=}{3}^{4 - 2}hfill & & & hfill frac{{5}^{2}}{{5}^{3}}stackrel{?}{=}frac{1}{{5}^{3 - 2}}hfill frac{81}{9}stackrel{?}{=}{3}^{2}hfill & & & hfill frac{25}{125}stackrel{?}{=}frac{1}{{5}^{1}}hfill 9=9 hfill & & & hfill frac{1}{5}=frac{1}{5}hfill end{array}[/latex]
When we work with numbers and the exponent is less than or equal to [latex]3[/latex], we will apply the exponent. When the exponent is greater than [latex]3[/latex] , we leave the answer in exponential form.
example
Simplify:
1. [latex]Largefrac{{x}^{10}}{{x}^{8}}[/latex]
2. [latex]Largefrac{{2}^{9}}{{2}^{2}}[/latex]
Solution
To simplify an expression with a quotient, we need to first compare the exponents in the numerator and denominator.
| 1. | |
| Since 10 > 8, there are more factors of [latex]x[/latex] in the numerator. | [latex]Largefrac{{x}^{10}}{{x}^{8}}[/latex] |
| Use the quotient property with [latex]m>n,Largefrac{{a}^{m}}{{a}^{n}}normalsize ={a}^{m-n}[/latex] . | [latex]{x}^{color{red}{10-8}}[/latex] |
| Simplify. | [latex]{x}^{2}[/latex] |
| 2. | |
| Since 9 > 2, there are more factors of 2 in the numerator. | [latex]Largefrac{{2}^{9}}{{2}^{2}}[/latex] |
| Use the quotient property with [latex]m>n,Largefrac{{a}^{m}}{{a}^{n}}normalsize ={a}^{m-n}[/latex]. | [latex]{2}^{color{red}{9-2}}[/latex] |
| Simplify. | [latex]{2}^{7}[/latex] |
Notice that when the larger exponent is in the numerator, we are left with factors in the numerator.
example
Simplify:
1. [latex]Largefrac{{b}^{10}}{{b}^{15}}[/latex]
2. [latex]Largefrac{{3}^{3}}{{3}^{5}}[/latex]
Solution
To simplify an expression with a quotient, we need to first compare the exponents in the numerator and denominator.
| 1. | |
| Since [latex]15>10[/latex], there are more factors of [latex]b[/latex] in the denominator. | [latex]Largefrac{{b}^{10}}{{b}^{15}}[/latex] |
| Use the quotient property with [latex]n>m,Largefrac{{a}^{m}}{{a}^{n}}normalsize =Largefrac{1}{{a}^{n-m}}[/latex]. | [latex]Largefrac{color{red}{1}}{{b}^{color{red}{15-10}}}[/latex] |
| Simplify. | [latex]Largefrac{1}{{b}^{5}}[/latex] |
| 2. | |
| Since [latex]5>3[/latex], there are more factors of [latex]3[/latex] in the denominator. | [latex]Largefrac{{3}^{3}}{{3}^{5}}[/latex] |
| Use the quotient property with [latex]n>m,Largefrac{{a}^{m}}{{a}^{n}}normalsize =Largefrac{1}{{a}^{n-m}}[/latex]. | [latex]Largefrac{color{red}{1}}{{3}^{color{red}{5-3}}}[/latex] |
| Simplify. | [latex]Largefrac{1}{{3}^{2}}[/latex] |
| Apply the exponent. | [latex]Largefrac{1}{9}[/latex] |
Notice that when the larger exponent is in the denominator, we are left with factors in the denominator and [latex]1[/latex] in the numerator.
Now let’s see if you can determine when you will end up with factors in the denominator, and when you will end up with factors in the numerator.
example
Simplify:
1. [latex]Largefrac{{a}^{5}}{{a}^{9}}[/latex]
2. [latex]Largefrac{{x}^{11}}{{x}^{7}}[/latex]
Quotient Property Khan
Solution
| 1. | |
| Since [latex]9>5[/latex], there are more [latex]a[/latex] ‘s in the denominator and so we will end up with factors in the denominator. | [latex]Largefrac{{a}^{5}}{{a}^{9}}[/latex] |
| Use the Quotient Property for [latex]n>m,Largefrac{{a}^{m}}{{a}^{n}}normalsize =Largefrac{1}{{a}^{n-m}}[/latex]. | [latex]Largefrac{color{red}{1}}{{a}^{color{red}{9-5}}}[/latex] |
| Simplify. | [latex]Largefrac{1}{{a}^{4}}[/latex] |
| 2. | |
| Notice there are more factors of [latex]x[/latex] in the numerator, since 11 > 7. So we will end up with factors in the numerator. | [latex]Largefrac{{x}^{11}}{{x}^{7}}[/latex] |
| Use the Quotient Property for [latex]m>n,Largefrac{{a}^{m}}{{a}^{n}}normalsize ={a}^{n-m}[/latex]. | [latex]{x}^{color{red}{11-7}}[/latex] |
| Simplify. | [latex]{x}^{4}[/latex] |
Watch the following video for more examples of how to simplify quotients that contain exponents. Pay attention to the last example where we demonstrate the difference between subtracting terms with exponents, and subtracting exponents to simplify a quotient.
Simplify Expressions with Zero Exponents
A special case of the Quotient Property is when the exponents of the numerator and denominator are equal, such as an expression like [latex]Largefrac{{a}^{m}}{{a}^{m}}[/latex]. From earlier work with fractions, we know that
[latex]Largefrac{2}{2}normalsize =1Largefrac{17}{17}normalsize =1Largefrac{-43}{-43}normalsize =1[/latex]
In words, a number divided by itself is [latex]1[/latex]. So [latex]Largefrac{x}{x}normalsize =1[/latex], for any [latex]x[/latex] ( [latex]xne 0[/latex] ), since any number divided by itself is [latex]1[/latex].
The Quotient Property of Exponents shows us how to simplify [latex]Largefrac{{a}^{m}}{{a}^{n}}[/latex] when [latex]m>n[/latex] and when [latex]n<m[/latex] by subtracting exponents. What if [latex]m=n[/latex] ?
Now we will simplify [latex]Largefrac{{a}^{m}}{{a}^{m}}[/latex] in two ways to lead us to the definition of the zero exponent.
Consider first [latex]Largefrac{8}{8}[/latex], which we know is [latex]1[/latex].
| [latex]Largefrac{8}{8}normalsize =1[/latex] | |
| Write [latex]8[/latex] as [latex]{2}^{3}[/latex] . | [latex]Largefrac{{2}^{3}}{{2}^{3}}normalsize =1[/latex] |
| Subtract exponents. | [latex]{2}^{3 - 3}=1[/latex] |
| Simplify. | [latex]{2}^{0}=1[/latex] |
We see [latex]Largefrac{{a}^{m}}{{a}^{n}}[/latex] simplifies to a [latex]{a}^{0}[/latex] and to [latex]1[/latex] . So [latex]{a}^{0}=1[/latex] .
Zero Exponent
If [latex]a[/latex] is a non-zero number, then [latex]{a}^{0}=1[/latex].
Any nonzero number raised to the zero power is [latex]1[/latex].
In this text, we assume any variable that we raise to the zero power is not zero.
example
Simplify:
1. [latex]{12}^{0}[/latex]
2. [latex]{y}^{0}[/latex]
Solution
The definition says any non-zero number raised to the zero power is [latex]1[/latex].
| 1. | |
| [latex]{12}^{0}[/latex] | |
| Use the definition of the zero exponent. | [latex]1[/latex] |
| 2. | |
| [latex]{y}^{0}[/latex] | |
| Use the definition of the zero exponent. | [latex]1[/latex] |
Now that we have defined the zero exponent, we can expand all the Properties of Exponents to include whole number exponents.
What about raising an expression to the zero power? Let’s look at [latex]{left(2xright)}^{0}[/latex]. We can use the product to a power rule to rewrite this expression.
| [latex]{left(2xright)}^{0}[/latex] | |
| Use the Product to a Power Rule. | [latex]{2}^{0}{x}^{0}[/latex] |
| Use the Zero Exponent Property. | [latex]1cdot 1[/latex] |
| Simplify. | [latex]1[/latex] |
This tells us that any non-zero expression raised to the zero power is one.
example
Simplify: [latex]{left(7zright)}^{0}[/latex].
Show SolutionSolution
| [latex]{left(7zright)}^{0}[/latex] | |
| Use the definition of the zero exponent. | [latex]1[/latex] |
Now let’s compare the difference between the previous example, where the entire expression was raised to a zero exponent, and what happens when only one factor is raised to a zero exponent.
example
Simplify:
1. [latex]{left(-3{x}^{2}yright)}^{0}[/latex]
2. [latex]-3{x}^{2}{y}^{0}[/latex]
Solution
| 1. | |
| The product is raised to the zero power. | [latex]{left(-3{x}^{2}yright)}^{0}[/latex] |
| Use the definition of the zero exponent. | [latex]1[/latex] |

| 2. | |
| Notice that only the variable [latex]y[/latex] is being raised to the zero power. | [latex]{-3{x}^{2}y}^{0}[/latex] |
| Use the definition of the zero exponent. | [latex]-3{x}^{2}cdot 1[/latex] |
| Simplify. | [latex]-3{x}^{2}[/latex] |
Now you can try a similar problem to make sure you see the difference between raising an entire expression to a zero power and having only one factor raised to a zero power.
In the next video we show some different examples of how you can apply the zero exponent rule.
Simplify Quotients Raised to a Power
Now we will look at an example that will lead us to the Quotient to a Power Property.
| [latex]{left(Largefrac{x}{y}normalsizeright)}^{3}[/latex] | |
| This means | [latex]Largefrac{x}{y}normalsizecdotLargefrac{x}{y}normalsizecdot Largefrac{x}{y}[/latex] |
| Multiply the fractions. | [latex]Largefrac{xcdot xcdot x}{ycdot ycdot y}[/latex] |
| Write with exponents. | [latex]Largefrac{{x}^{3}}{{y}^{3}}[/latex] |
Notice that the exponent applies to both the numerator and the denominator.
We see that [latex]{left(frac{x}{y}normalsizeright)}^{3}[/latex] is [latex]Largefrac{{x}^{3}}{{y}^{3}}[/latex].
Quotient Properties Of Exponents
[latex]begin{array}{ccccc}text{We write:}hfill & & & & {left(frac{x}{y}right)}^{3}hfill & & & & frac{{x}^{3}}{{y}^{3}}hfill end{array}[/latex]
This leads to the Quotient to a Power Property for Exponents.
Quotient to a Power Property of Exponents
If [latex]a[/latex] and [latex]b[/latex] are real numbers, [latex]bne 0[/latex], and [latex]m[/latex] is a counting number, then
[latex]{left(Largefrac{a}{b}normalsizeright)}^{m}=Largefrac{{a}^{m}}{{b}^{m}}[/latex]
To raise a fraction to a power, raise the numerator and denominator to that power.
An example with numbers may help you understand this property:
[latex]Largefrac{2}{3}^3[/latex] = [latex]Largefrac{{2}^{3}}{{3}^{3}}[/latex] = [latex]Largefrac{8}{27}[/latex]
example
Simplify:
1. [latex]{left(Largefrac{5}{8}normalsizeright)}^{2}[/latex]
2. [latex]{left(Largefrac{x}{3}normalsizeright)}^{4}[/latex]
3. [latex]{left(Largefrac{y}{m}normalsizeright)}^{3}[/latex]
Quotient Property Problems
Solution
| 1. | |
| [latex]Large(frac{5}{8})^2[/latex] | |
| Use the Quotient to a Power Property, [latex]{Largeleft(frac{a}{b}right)}^{m}normalsize =Largefrac{{a}^{m}}{{b}^{m}}[/latex] . | [latex]Largefrac{5^{color{red}{2}}}{8^{color{red}{2}}}[/latex] |
| Simplify. | [latex]Largefrac{25}{64}[/latex] |
| 2. | |
| [latex]Large(frac{x}{3})^4[/latex] | |
| Use the Quotient to a Power Property, [latex]{Largeleft(frac{a}{b}right)}^{m}normalsize =Largefrac{{a}^{m}}{{b}^{m}}[/latex] . | [latex]Largefrac{x^{color{red}{4}}}{3^{color{red}{4}}}[/latex] |
| Simplify. | [latex]Largefrac{x^4}{81}[/latex] |
| 3. | |
| [latex]Large(frac{y}{m})^3[/latex] | |
| Raise the numerator and denominator to the third power. | [latex]Largefrac{y^{3}}{m^{3}}[/latex] |
Quotient Properties Of Exponents
For more examples of how to simplify a quotient raised to a power, watch the following video.